 Do G1/PE
Do G1/PE
O Ibope divulgou, hoje, o resultado da segunda pesquisa do instituto sobre o segundo turno da eleição para prefeito do Recife. O levantamento foi realizado entre os dias 23 e 25 de novembro e tem margem de erro de 3 pontos percentuais, para mais ou para menos.
Os resultados foram os seguintes:
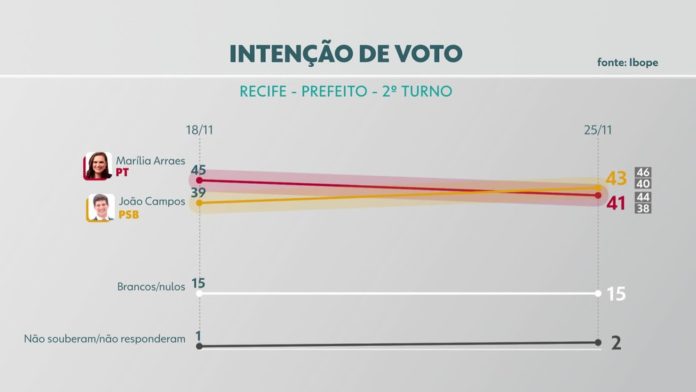
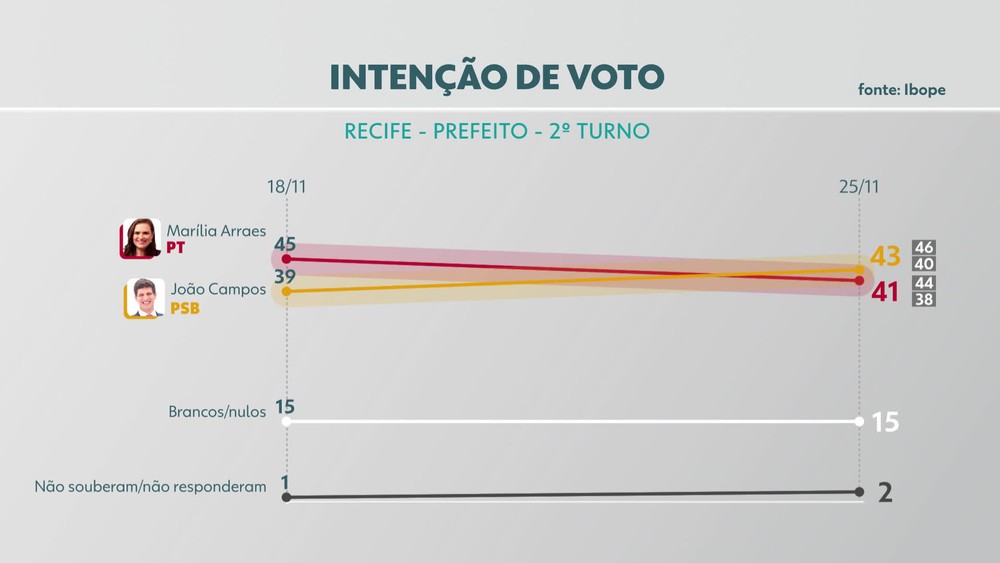
- João Campos (PSB): 43%
- Marília Arraes (PT): 41%
- Em branco/nulo: 15%
- Não sabe/não respondeu: 2%
Em relação ao levantamento anterior do Ibope, divulgado em 18 de novembro:
- João Campos (PSB): tinha 39% e subiu para 43%
- Marília Arraes (PT): tinha 45% e desceu para 41%
- Em branco/nulo: se manteve em 15%
- Não sabe/não respondeu: subiu de 1% para 2%
De acordo com o Ibope, persiste um empate técnico entre os candidatos, mas agora com a inversão da vantagem numérica em relação à pesquisa anterior. A diferença entre ambos é de apenas dois pontos percentuais e menor que a margem de erro da pesquisa, que é de três pontos percentuais.
Votos válidos
Nos votos válidos, os resultados foram os seguintes:
- João Campos (PSB): 51%
- Marília Arraes (PT): 49%
Em relação ao levantamento anterior do Ibope, divulgado em 18 de novembro:
- João Campos (PSB): tinha 47% e subiu para 51%
- Marília Arraes (PT): tinha 53% e caiu para 49%
Para calcular os votos válidos, são excluídos da amostra os votos brancos, os nulos e os eleitores que se declaram indecisos. O procedimento é o mesmo utilizado pela Justiça Eleitoral para divulgar o resultado oficial da eleição. Para vencer no 2º turno, um candidato precisa de 50% dos votos válidos mais um voto.
Intenção de voto espontânea
- João Campos (PSB): 40%
- Marília Arraes (PT): 38%
- Outros: 1%
- Branco/nulo: 18%
- Não sabe/não respondeu: 4%
Sobre a pesquisa
Margem de erro: 3 pontos percentuais para mais ou para menos
Entrevistados: 1.001 eleitores do Recife
Quando a pesquisa foi feita: entre 23 e 25 de novembro
Registro no TRE: PE?04600/2020
Nível de confiança: 95%
Contratantes da pesquisa: TV Globo e “Jornal do Commercio”
O nível de confiança da pesquisa é de 95%. Isso quer dizer que há uma probabilidade de 95% de os resultados retratarem a realidade, considerando a margem de erro, que é de 3 pontos, para mais ou para menos.